Vamos a programar #60 - Los números de Fibonacci (Ver. C)
Hola de nuevo a todos, el día de hoy vamos a ver un poco acerca de la sucesión de Fibonacci. Hace poco alguien me comentó que en la universidad, le dejaron de tarea hacer un programa en C que calculara el valor "n" de un número en la sucesión de Fibonacci.
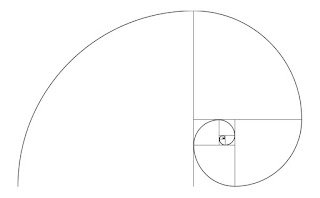
Antes de continuar, vamos a ver que es esta sucesion.
El propósito del programa era encontrar una manera de hacerlo de forma secuencial y otra de forma re-cursiva. Partiendo de eso, podemos crear un programa cómo el que sigue:
El programa consta de dos funciones, una de ellas es "FibonacciNumbersRec" (Rec es por Recursive) y la otra es "FibonacciNumbersIt" (It por Iterative). Para la función "FibonacciNumbersRec", primeramente comprobamos si el parámetro "n" es cualquiera de los números 1 o 0, si es el caso, la función devuelve "n" cómo resultado, si no es el caso anterior, la función se mandará a llamar a si misma con el parámetro "n = n - 1" y al resultado de esto, se le sumará el valor que resulta de llamarse a si misma con parámetro de "n = n -2"; el valor que regresa la función será el resultado de sumar los casos anteriores.
Para evitar la recursividad, podemos aprovechar que la sucesión depende de los dos valores anteriores inmediatos, por lo que podemos hacer todo en un ciclo "for" y usando las variables auxiliares "v1","v2 y "v3". Cómo la sucesión comienza con 1 y con 0, le asignamos esos valores a "v1" y a "v2", el resultado para ese paso dentro de la sucesión, sera la suma "v1" + "v2", los asignamos a "v3" y tomando en cuenta lo mencionado hace un momento, le asignamos a "v1" el valor que tiene "v2" y a "v2" le asignamos el valor de "v3". Todo esto lo hacemos hasta que el iterador llegue al valor del parámetro "n". Finalmente la función regresará cómo resultado el valor de "v1".
Y bien, con el código anterior hemos demostrado que hay más de una forma para llegar al mismo resultado. Muchas veces es más fácil hacer uso de la recursividad, pero si por alguna razón no debemos (o no disponemos, dependiendo del lenguaje) usarla, siempre hay formas de encontrar una solución.
El código, al igual que el del post anterior, puedes copiarlo y probarlo en el compilador online.
Y bien. por ahora es todo, los leo luego.
Antes de continuar, vamos a ver que es esta sucesion.
En matemáticas, la sucesión de Fibonacci es la siguiente sucesión infinita de números naturales: 0,1,1,2,3,5,8,13,21,34,55, … La sucesión comienza con los números 0 y 1,2 y a partir de estos, «cada término es la suma de los dos anteriores», es la relación de recurrencia que la define. A los elementos de esta sucesión se les llama números de Fibonacci. Esta sucesión fue descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci. Tiene numerosas aplicaciones en ciencias de la computación, matemática y teoría de juegos. También aparece en configuraciones biológicas, como por ejemplo en las ramas de los árboles, en la disposición de las hojas en el tallo, en las flores de alcachofas y girasoles, en las inflorescencias del brécol romanesco y en la configuración de las piñas de las coníferas. De igual manera, se encuentra en la estructura espiral del caparazón de algunos moluscos, como el nautilus. Wikipedia/SucesionDeFibonacci.Para ponerlo de manera sencilla, para calcular el valor de la sucesión, debemos de sumar los dos números previos, excepto cuando el valor de n sea 0 o 1, a partir de "n = 2", es cuando debemos de empezar a sumar por lo que tendríamos algo similar a lo siguiente:
#include <stdio.h>
long FibonacciNumbersRec(int n)
{
if (n == 0 || n== 1 )
return n;
else
return (FibonacciNumbersRec(n - 1) + FibonacciNumbersRec(n - 2));
}
long FibonacciNumbersIt(int n)
{
long v1 = 0;
long v2 = 1;
long v3, i;
for(i = 1; i <= n; i++)
{
v3 = v1+v2;
v1 = v2;
v2 = v3;
}
return v1;
}
int main()
{
printf("%4d\n", FibonacciNumbersIt(6));
printf("%4d\n", FibonacciNumbersRec(6));
}
El programa consta de dos funciones, una de ellas es "FibonacciNumbersRec" (Rec es por Recursive) y la otra es "FibonacciNumbersIt" (It por Iterative). Para la función "FibonacciNumbersRec", primeramente comprobamos si el parámetro "n" es cualquiera de los números 1 o 0, si es el caso, la función devuelve "n" cómo resultado, si no es el caso anterior, la función se mandará a llamar a si misma con el parámetro "n = n - 1" y al resultado de esto, se le sumará el valor que resulta de llamarse a si misma con parámetro de "n = n -2"; el valor que regresa la función será el resultado de sumar los casos anteriores.
Para evitar la recursividad, podemos aprovechar que la sucesión depende de los dos valores anteriores inmediatos, por lo que podemos hacer todo en un ciclo "for" y usando las variables auxiliares "v1","v2 y "v3". Cómo la sucesión comienza con 1 y con 0, le asignamos esos valores a "v1" y a "v2", el resultado para ese paso dentro de la sucesión, sera la suma "v1" + "v2", los asignamos a "v3" y tomando en cuenta lo mencionado hace un momento, le asignamos a "v1" el valor que tiene "v2" y a "v2" le asignamos el valor de "v3". Todo esto lo hacemos hasta que el iterador llegue al valor del parámetro "n". Finalmente la función regresará cómo resultado el valor de "v1".
Y bien, con el código anterior hemos demostrado que hay más de una forma para llegar al mismo resultado. Muchas veces es más fácil hacer uso de la recursividad, pero si por alguna razón no debemos (o no disponemos, dependiendo del lenguaje) usarla, siempre hay formas de encontrar una solución.
El código, al igual que el del post anterior, puedes copiarlo y probarlo en el compilador online.
Y bien. por ahora es todo, los leo luego.
No hay comentarios.