Vamos a programar #55 - Los números de Munchhausen (ver. C#)
Hola de nuevo a todos, el día de hoy vamos a ver los números de Munchhausen y cómo probar la conjetura usando código en C#.
Antes que nada, veamos la definicion de los número de Munchhausen segun wikipedia:
El código anterior consta de cuatro funciones, pero solo la función "IsMunchhausenNumber()" es la que hace el trabajo, el resto solo son para poder usar la aplicación y que esta no se bloquee cuando se realice el proceso.
La función "IsMunchhausenNumber" recibe un parámetro del tipo "string" que será la cadena de texto que representa el número que se va a probar; decidí tomar directamente el parámetro cómo un "string" debido a que cuando recuperamos el número de la caja de texto, este sera de ese tipo, entonces convertirlo y luego hacer una conversión más para poder separarlo en los dígitos, significa doble trabajo.
Dentro de la función, convertimos el parámetro ingresado en un "array" del tipo "char", cada elemento representara un dígito del número ingresado. Luego para poder hacer los cálculos con cada dígito, a cada valor del tipo "char" le restamos 48 para obtener su valor real. Hay que recordar que el tipo "char" es esencialmente igual al tipo "byte" por lo que podemos restar (aunque habría que hacer la conversión implícita pero meh). La razón por la que se resta 48, es porque el número cero, esta en el lugar 48, el uno es 49 y así sucesivamente hasta el número nueve. Si intentamos convertir el valor del tipo "char" "0" a uno del tipo "int", este regresará 48, por lo que hacer la resta directamente resulta más fácil.
Después con los numero ya separados se hace la suma siguiendo las reglas de la conjetura y se compara el valor de la variable usada para hacer la suma con el número ingresado cómo parámetro; si estos son iguales entonces la función devuelve un valor del tipo "bool" "true", en caso contrario devuelve "false".
Para probar los número, se hace uso de la función "TestNumbers". Esta función recibe tres parámetros, el primero del tipo "int" que servirá cómo limite mínimo para empezar a probar los números. El segundo parámetro también del tipo "int" sirve para marcar el limite máximo hasta cual se van a probar los números, finalmente el tercer parámetro del tipo "bool", servirá par filtrar los resultados; solo cuando este sea "true", todos los resultados sin importar que cumplan la conjetura, se agregan a la lista de salida, en caso contrario, solo los que la cumplen son agregados.
Y bien, por ahora es todo en futuros post veremos que hacen el resto de las funciones (que de seguro habrás notado que aparecen en varios de los programas del blog) y probablemente al igual que algunos otros de los programas, crearemos versiones para android en java y web en javascript. Cómo de costumbre, puedes descargar el código fuente de mi dropbox para que lo pruebes.
Los leo luego
Antes que nada, veamos la definicion de los número de Munchhausen segun wikipedia:
El término fue acuñado por el ingeniero de software y matemático holandés Daan van Berkel en 2009. El nombre se debe a que cada dígito está "elevado" por sí mismo, esto evoca la historia de Barón Munchausen que se elevó a sí mismo hacia arriba jalando su propia coleta. Los números narcisistas siguen una regla similar, pero en el caso de los números narcisistas la potencia de los dígitos es fija, siendo elevados a la potencia del número de dígitos en el número.En resumidas cuentas, se trata de tomar un número y separar cada dígito y este a su vez elevarlo a la potencia que será el mismo dígito. Antes de continuar, actualmente solo hay dos números conocidos que cumplen la conjetura. uno de ellos es el número 1 puesto que:
- 1 = 1^1 = 1.
- 3435 = 3^3 + 4^4 + 3^3 + 5^5 = 27 + 256 + 27 + 3125 = 3435.
El código.
El código en C# que sirve para probar la conjetura es el siguiente:
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Windows.Forms;
using System.Threading;
namespace Munchhausen
{
public partial class FrmMain : Form
{
private bool IsBusy = false;
private delegate void UpdateListDelegate(string Value);
private void UpdateList(string Value)
{
if (LBResults.InvokeRequired)
LBResults.Invoke(new UpdateListDelegate(UpdateList), Value);
else
LBResults.Items.Add(Value);
}
private bool IsMunchhausenNumber(string Number)
{
int Value = 0;
int CurrentNumber = 0;
char[] Digits = Number.ToCharArray();
for (int i = 0; i < Digits.Length; i++)
{
CurrentNumber = Digits[i] - 48;
Value += (int)Math.Pow(CurrentNumber,CurrentNumber);
}
if (Number == Value.ToString())
return true;
else
return false;
}
private void TestNumbers(int BeginNumber, int EndNumber, bool SHowAll)
{
for (int i = BeginNumber; i <= EndNumber; i++)
{
if (IsMunchhausenNumber(i.ToString()))
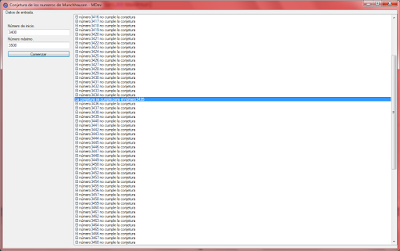
UpdateList("La conjetura se cumple para el número " + i);
if (SHowAll)
UpdateList("El número " + i + " no cumple la conjetura");
}
IsBusy = false;
}
private void RunWork(int Minimum, int Maximun, bool ShowAll = false)
{
Thread DoWork = new Thread(new ThreadStart(() => TestNumbers(Minimum, Maximun,ShowAll)));
IsBusy = true;
DoWork.Start();
}
public FrmMain()
{
InitializeComponent();
}
private void BtnStart_Click(object sender, EventArgs e)
{
LBResults.Items.Clear();
if (!IsBusy)
RunWork(int.Parse(TxtMinNumber.Text), int.Parse(TxtMaxNumber.Text),CHKShowTrue.Checked);
else
MessageBox.Show("Hay una operación en proceso, espera","MDev",MessageBoxButtons.OK,MessageBoxIcon.Exclamation);
}
private void FrmMain_FormClosing(object sender, FormClosingEventArgs e)
{
if (IsBusy == true)
{
MessageBox.Show("No se puede salir ahora","MDev", MessageBoxButtons.OK, MessageBoxIcon.Exclamation);
e.Cancel = true;
}
}
}
}
El código anterior consta de cuatro funciones, pero solo la función "IsMunchhausenNumber()" es la que hace el trabajo, el resto solo son para poder usar la aplicación y que esta no se bloquee cuando se realice el proceso.
La función "IsMunchhausenNumber" recibe un parámetro del tipo "string" que será la cadena de texto que representa el número que se va a probar; decidí tomar directamente el parámetro cómo un "string" debido a que cuando recuperamos el número de la caja de texto, este sera de ese tipo, entonces convertirlo y luego hacer una conversión más para poder separarlo en los dígitos, significa doble trabajo.
Dentro de la función, convertimos el parámetro ingresado en un "array" del tipo "char", cada elemento representara un dígito del número ingresado. Luego para poder hacer los cálculos con cada dígito, a cada valor del tipo "char" le restamos 48 para obtener su valor real. Hay que recordar que el tipo "char" es esencialmente igual al tipo "byte" por lo que podemos restar (aunque habría que hacer la conversión implícita pero meh). La razón por la que se resta 48, es porque el número cero, esta en el lugar 48, el uno es 49 y así sucesivamente hasta el número nueve. Si intentamos convertir el valor del tipo "char" "0" a uno del tipo "int", este regresará 48, por lo que hacer la resta directamente resulta más fácil.
Después con los numero ya separados se hace la suma siguiendo las reglas de la conjetura y se compara el valor de la variable usada para hacer la suma con el número ingresado cómo parámetro; si estos son iguales entonces la función devuelve un valor del tipo "bool" "true", en caso contrario devuelve "false".
Para probar los número, se hace uso de la función "TestNumbers". Esta función recibe tres parámetros, el primero del tipo "int" que servirá cómo limite mínimo para empezar a probar los números. El segundo parámetro también del tipo "int" sirve para marcar el limite máximo hasta cual se van a probar los números, finalmente el tercer parámetro del tipo "bool", servirá par filtrar los resultados; solo cuando este sea "true", todos los resultados sin importar que cumplan la conjetura, se agregan a la lista de salida, en caso contrario, solo los que la cumplen son agregados.
Y bien, por ahora es todo en futuros post veremos que hacen el resto de las funciones (que de seguro habrás notado que aparecen en varios de los programas del blog) y probablemente al igual que algunos otros de los programas, crearemos versiones para android en java y web en javascript. Cómo de costumbre, puedes descargar el código fuente de mi dropbox para que lo pruebes.
Los leo luego











No hay comentarios.